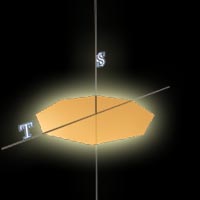Диэдр

Назовем экватором большой круг, на котором лежат n вершин диэдра, и отметим два  полюса. Диэдр переходит в себя под действием циклической группы из n вращений, для которой оба полюса неподвижны. Однако группа вращений диэдра этим не исчерпывается. Отметим на экваторе точку посередине между двумя последовательными вершинами диэдра; назовем ее серединой ребра диэдра. Диаметр, проходящий через вершину диэдра или через середину его ребра, является осью симметрии второго порядка для диэдра. Всего имеется n таких осей, если n нечетно, каждая  из них соединяет вершину с серединой ребра; если n четно, то оси разбиваются на две категории соответственно тому, проходят ли они через вершины или через середины ребра диэдра. Во всех случаях диэдр переходит в себя при поворотах на 180° вокруг каждой из n осей. Таким образом, помимо циклической группы из n вращений имеется ещё n поворотов периода 2. Можно сказать, что группа диэдра не содержит других вращений, кроме перечисленных выше. Общий принцип: две операции сопряжены, если они действуют одинаковым образом на две сопряженные фигуры. Применение этого принципа к нашему случаю ясно. В качестве основных фигур рассмотрим полюсы диэдра. В подгруппе главных вращении сопряжены между собой повороты на углы 2kp/n и -2kp/n, а среди поворотов на 180° вокруг осой второго порядка для нечетного n все сопряжены друг другу, а для четного n есть два класса. Первое утверждение соответствует тому, что два со­пряженных поворота выглядят одинаково с точки зрения наблюдателей, помещенных в двух полюсах, а вто­рое - тому, что оси второго порядка либо все сопряжены друг другу, либо для четного n распадаются на два клас­са сопряженных объектов.

Квадратичная группа

            Вначале мы предполагали, что n > 2. Если n = 2, фигура диэдра теряет смысл как многогранник, поскольку две вершины могут быть соединены бесчисленным множеством больших окружностей. В соответствии с этим мы получаем в качестве группы вращений так называемую непрерывную группу. Хотя теория таких групп весьма интересна и важна во многих отношениях, в на­ших исследованиях она не будет играть роли. Поэтому в случае n = 2 сделаем фигуру диэдра определенной, выбрав из бесчисленного множества больших окружностей, соединяющих две вершины, один экватор, и зафиксируем соответствующие два полюса. Тогда главная ось вместе с двумя осями второго порядка образует ортогональную триаду, и мы получаем в точном соответствии со сказанным в предыдущем параграфе группу из 2n=4 вращений. Если ввести обычным образом координаты с по­мощью этих трех осей, то точки х, у, z переводятся ди­эдральными вращениями в точки

  x, -y, -z

-x, y, -z

-x, -y, z

          Наша группа состоит, помимо единицы, исключительно из элементов второго порядка и только слу­чайное обстоятельство заставляет нас выделять главную ось среди трех равноправных осей. Поэтому, чтобы не связывать эту группу с конфигурацией диэдра, будем называть ее квадратичной группой. Эта группа, как легко проверить, коммутативна. Поэтому каждый элемент ее сопряжен только с самим собой. Разложение квадратичной группы получается, если выбрать лю­бую подгруппу из двух вращений, сохраняющих одну из трех осей.